I’ve always found procedurally generated landscapes to be really interesting. When well done, they create an infinte number of incredible places to explore. So, I decided to take a stab at implementing a common algorithm that outputs random heightmaps called Diamond-Square.

</img>

You’re probably reading this post because you’re interested in implementing Diamond-Square (DS) yourself, so let’s hop right into it. To see the algorithm in action, step-by-step, check out this great post by Paul Boxley.

Algorithm Overview

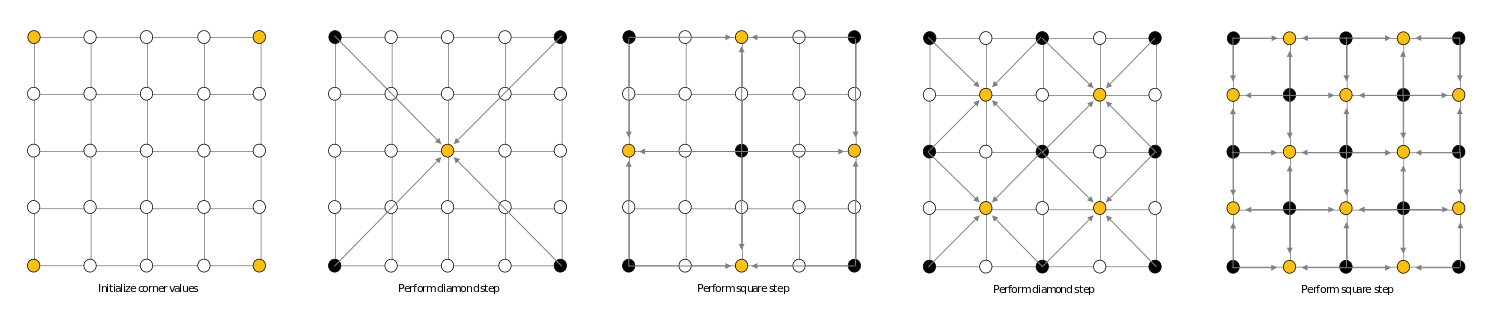
DS requires a 2D array of size 2^n + 1 (5x5, 17x17, 33x33, etc.). It begins with pre-seeded values in the four corners of the array. It then loops over progressively smaller step sizes, performing a ‘diamond step’ and then a ‘square step’ until each value in the array has been set.

The diamond step takes a square, finds the midpoint, and sets the midpoint to the average of the four corners plus a random value in some range. Imagine drawing lines from the four points to the midpoint, for every square in the array: you would create a diamond pattern (hence the name!).

The square step takes a diamond, finds the midpoint, and pulls in the average of the values of the points forming the corners of the diamond (plus a random value). Again, imagine drawing the lines from the corners to the midpoint: you’d create a square pattern.

The intution behind DS can be most easily seen in 1 dimension. Here’s a great explanation using midpoint-displacement to create a mountain range. That post also describes DS in detail, so definitely check it out. DS uses the same idea of midpoint-displacement, but in 2D. Starting with the four corner values, it finds the midpoint of that square, which generates diamonds. Then, it sets the value of the midpoint of each new diamond. This essentially displaces midpoint values (plus a random amount) the same way 1D midpoint-displacement does.

Pseudocode and Implementation

Now let’s look at some pseudocode to understand the details a bit better.

def diamond_square(width, height):
  # Set up the array of z-values
  let A = a width*height 2D array of 0s
  pre-seed four corners of A with a value

  let step_size = width - 1
  let r = a random number within a range

  # Main loop
  while step_size > 1:
    loop over A
      do diamond_step for each square in A 

    loop over A
      do square_step for each diamond in A

    step_size /= 2
    reduce random range for r

def diamond_step(x, y, step_size, r):
  # Note: this assumes x, y is top-left of square
  #       but you can implement it how you like
  let avg = average of square corners step_size apart
  A[x + step_size/2][y + step_size/2] = avg + r

def square_step(x, y, step_size, r):
  # Note: x, y here are the middle of a diamond
  let avg = average of four corners of diamond 
  A[x][y] = avg + r

Now, the tricky part of implementing DS are the corner-cases found in the array manipulation, which the pseudocode doesn’t really highlight. But, it’s a good starting point. I recommend trying to implement DS yourself before looking at working source code - it’ll be more rewarding and a better learning experience. However, here’s an implementation I wrote and here’s another (cleaner, in my opinion) version.

Additional Resources

I found several nice resources for learning about procedural terrain generation while implementing this little project. Hopefully they’re of use to you as well.

StackOverflow post about getting started with procedural generation

A list of procedural generation algorithms